Before designing FIFO by myself, trying to understand Spinal m2sPipe.
前回、自力で FIFO の設計を試みましたが、直感的なやり方では設計が困難なことが分かりました。そこで、もう少し形式的な手法ということで、いくつか教科書をひっくり返し、Mealy マシンの設計について復習してみました。Google で検索するといろいろ出てくると思いますが、この説明の 13ページに出てくる図(Mealy と Moore マシンの比較)が少し分かりやすいかな、と思います。
しかしながら、自分で Mealy マシンを設計しようとすると、「状態」をどのように分類するか、という問題に突き当たります。FSM(状態遷移マシン)のように明確に状態を定義できるものであればやりやすいのですが、FIFO はちょっと(私には)難しいです。そこでまずは、SpinalHDL のライブラリにある Stream.m2sPipe() の実装を繙き、逆エンジニアリングしてみることにしました。
m2sPipe の真理値表を書いてみる
まず最初に、前回示した論理回路図を再掲します。
続いて、解読(?)した真理値表を示しますが、表が汚らしくならないように、少し略記をします。
- rV: valid ラインに繋がっている D-FF の出力(つまり内部状態)
- rP: payload ラインに繋がっている D-FF の出力(同)
- s.v: src.valid(.p は payload、.r は ready)
- d.v: sink.valid(d は destination のつもり)
- rV*, rP*: rV と rP の、次の(つまり 1クロック後の)状態
- NC: Don’t Care(SpinalHDL の Stream バスの定義より、valid が False の場合は ready や payload は Don’t Care になる)
- 1: True(T と F だと読みにくいので)
- 0: False(同)
- p0, p1: それぞれ payload の任意の値
真理値表です。最初(左端)が、状態および入力の全種類に対応するラベル、続いて 2桁が(現在の)状態、3桁が入力、2桁が次の状態、最後の 3桁が出力です。
| 状態 | 入力 | 次の状態 | 出力 | |||||||
| ラベル | rV | rP | s.v | s.p | d.r | rV* | rP* | d.v | d.p | s.r |
| A | 0 | p0 | 0 | NC | 0 (NC) | 0 | NC | 0 | p0 (NC) | 1 (NC) |
| (B) | 0 | p0 | 0 | NC | 1 (NC) | 0 | NC | 0 | p0 (NC) | 1 (NC) |
| C | 0 | p0 | 1 | p1 | 0 (NC) | 1 | p1 | 0 | p0 (NC) | 1 |
| (D) | 0 | p0 | 1 | p1 | 1 (NC) | 1 | p1 | 0 | p0 (NC) | 1 |
| E | 1 | p0 | 0 | NC | 0 | 1 | p0 | 1 | p0 | 0 (NC) |
| F | 1 | p0 | 0 | NC | 1 | 0 | NC | 1 | p0 | 1 (NC) |
| G | 1 | p0 | 1 | p1 | 0 | 1 | p0 | 1 | p0 | 0 |
| H | 1 | p0 | 1 | p1 | 1 | 1 | p1 | 1 | p0 | 1 |
ここで、ラベル B と D にカッコが付いているのは、B は A と同義であり、D は C と同義であるため、検討しなくて良いということです。なぜなら、d.r(sink.ready)が Don’t Care なので、d.r が True でも False でも同じ扱いなのです。
シミュレーションの波形と比べる
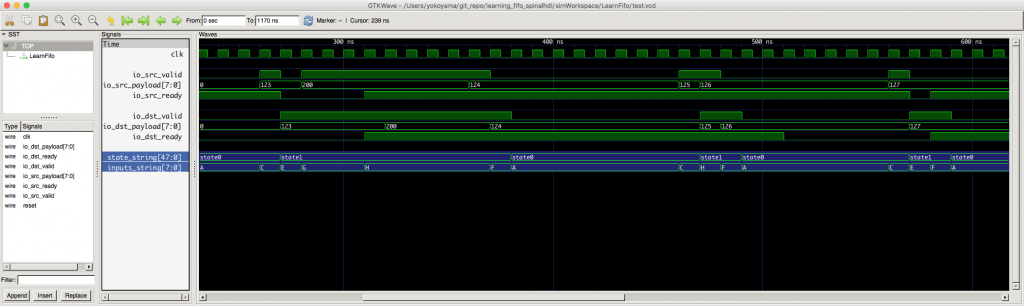
それでは、シミュレーション結果と比べてみましょう。上記真理値表のラベルと状態を合わせて出力するようにしてみました。クリックすると拡大できます。
state_string は、ここでは rV D-FF の内部状態を表しています。0(False) のときが state0 で、1(True)のときが state1 ですね。(このようなシミュレーション出力の方法については後述します。)
これを見ると、私のシミュレーション用テストベンチは、全ての可能な状態と入力を網羅できていることが分かりました。(結果オーライ?)
設計の解読結果の考察
次に、各状態と入力に対する出力論理について考察してみましょう。
まず最初に rV D-FF の内部状態ですが、
- 0(False): FIFO 内部には、「預かり中」のデータ(payload)を持っていない、つまり「FIFO が空」の状態
- 1(True): 反対に、FIFO 内部に「預かり中」のデータがある状態、つまり FIFO フルの状態
こう考えると、意外と素直な設計と言えるでしょう。ま、FIFO だから当たり前といえばそうですが、ここまで解読してみて、ようやく理解できたという気持ちです。
次に、各ラベルに対する状態遷移と出力の論理についてです。
- A: FIFO が空で、src.valid = False。この場合は状態変化せず、出力は dst.valid = False です。
- C: FIFO が空で、src.valid = True。この場合は、データの預かりが発生するので rV D-FF = 1 に遷移します。出力は、まだ dst.valid = False ですが、src.ready は True となり、データを預かったので、次サイクルで source は valid を落として(de-assert して)良いよ、ということになります。
- E: FIFO がフルで、src.valid = False かつ dst.ready = False。出力は dst.valid = True です。sink に対して、データの準備ができていることを伝えていますが、dst.ready = False なので rV D-FF = 0 に状態遷移できません。(データは預かったまま)
- F: FIFO がフルで、src.valid = False かつ dst.ready = True。出力は dst.valid = True です。sink に対して、データの準備ができていることを伝えており、また dst.ready = True なので、このサイクルでデータは sink が受け取れています。つまり、rV D-FF = 0 に状態遷移できます。
- G: FIFO がフルで、src.valid = True かつ dst.ready = False。つまり、まだデータを sink に引き渡せていないのに src.valid が True になってしまったということです。出力 dst.valid は True のまま、また、source からのデータを受け取れないので、src.ready = False となります。もちろん状態遷移はできません。
- H: FIFO がフルで、src.valid = True かつ dst.ready = True。dst.ready = True なので、このサイクルでデータは sink が受け取れています。次サイクルで source からのデータを受け取れるので、src.ready = True で示します。(src.valid が True で dst.ready が True だと、この状態 rV D-FF = 1 かつ、ラベル H の入力が連続し、結果として source から sink へ、1サイクル遅延で毎サイクルデータが転送されることになります。)
いかがでしょうか。期待通りの動作になっていそうですね。
それにしても、FIFO というのは意外と難しいものだということが分かりました。しかし、ここまで解読できれば、自分でも m2sPipe くらいは設計できそうな気もしてきますね。(無理かな?)
シミュレーション波形に状態を出力する方法
さて、上述の波形で状態を文字列で表示していますが、これはどうやるのでしょう。実は SpinalHDL には SpinalEnum という型が定義されており、それを使うことでシミュレーション結果に文字列を得ることができます。コードを示しておきます。あまり綺麗でないですが御容赦ください。
import spinal.core._
import spinal.lib._
object FifoState extends SpinalEnum {
val state0, state1 = newElement()
}
object FifoInput extends SpinalEnum {
val A, C, E, F, G, H, X = newElement()
}
class LearnFifo(
width_payload: Int
) extends Component {
val io = new Bundle {
val src = slave Stream (Bits(width_payload bits))
val dst = master Stream (Bits(width_payload bits))
}
val state = FifoState() // 状態
val inputs = FifoInput() // 入力ラベル
io.src.m2sPipe() >> io.dst
when(io.dst.valid) {
state := FifoState.state1
} otherwise {
state := FifoState.state0
}
inputs := FifoInput.X
when(state === FifoState.state0 && !io.src.valid) {
inputs := FifoInput.A
}
when(state === FifoState.state0 && io.src.valid) {
inputs := FifoInput.C
}
when(state === FifoState.state1 && !io.src.valid && !io.src.ready) {
inputs := FifoInput.E
}
when(state === FifoState.state1 && !io.src.valid && io.src.ready) {
inputs := FifoInput.F
}
when(state === FifoState.state1 && io.src.valid && !io.src.ready) {
inputs := FifoInput.G
}
when(state === FifoState.state1 && io.src.valid && io.src.ready) {
inputs := FifoInput.H
}
}
今日はここまで。