Learning logic circuits by Minecraft (part 4).
前回に続き、マイクラで論理回路(ろんりかいろ)を学ぼう、の第 4回目です。お待たせしました。ようやく論理回路の説明に入ります。少しむずかしい話になりますので、しっかりついてきてくださいね!
シリーズの記事一覧は、こちらです。
このページをふりがな付きで読みたいときは、こちらをクリックしてください!(「ひらひらのひらがなめがね」さんのサービスを使わせて頂いています。)
もし、分からないことがあるときは、お父さんやお母さんに相談しても良いでしょう。このページの終わりに問い合わせフォームがありますので、気軽にしつもんしてくださいね。(わたしも、うまく説明できていないところは、どんどん直したいと思っています。)
もう一つ。本当は説明を全てふりがな付きで書けたら良いのですが、読んでいる方が何年生か知る方法がないので、専門(せんもん)用語以外は全て漢字で書いています。漢字の文章にふりがなを付けてくれる便利なウェブサイトもありますので、ぜひ活用してください。
論理回路の記号
論理回路は普通、回路図というものを使って設計します。回路図を描くには、いろいろな記号の決まり事があります。
皆さんは、学校で「地図」について勉強したことがありますね。こちらに地図記号の一覧がありますが、少し復習してみましょう。
これは、皆さんがよく知っている「学校」の記号ですね。

次は、消防署の記号です。

これと似たように、回路図を描くときにもいろいろな記号を使います。今回は、論理回路を描くときに使う、重要な 3つの記号について説明します。
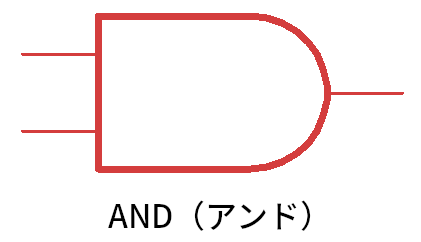
AND(アンド)回路
これは、AND(アンド)という記号です。論理積(ろんりせき)とも言います。意味は、後で説明しましょう。
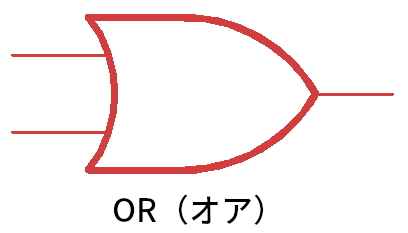
OR(オア)回路
これは OR(オア)です。論理和(ろんりわ)とも言います。
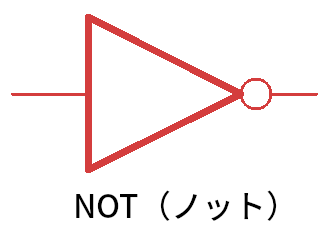
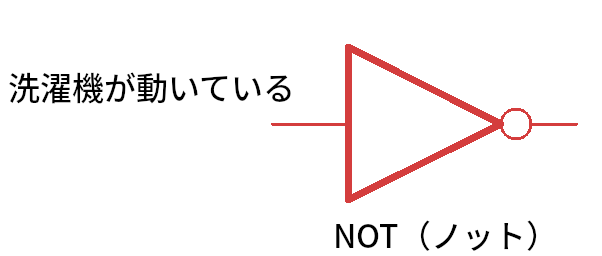
NOT(ノット)回路
これは NOT(ノット)です。インバータ、論理否定(ろんりひてい)とも言います。
論理回路ってなんだろう?
さて、論理回路とはなんでしょう。
皆さんが持っているスマートフォン、タブレット、パソコン、さらには、今の洗濯機や冷蔵庫、エアコン、自動車などには、全て「電子回路」というものが入っています。電子回路の中でも、いろいろと複雑な判断(はんだん)をするための回路を「論理回路」と言います。
例えばいま、あなたのお部屋の中に、次のような「判断」ができる論理回路の入った、頭のいい照明器具(ライト)があったとしましょう。
- 「今が夜で」、そして「部屋の中に人がいたら」、自動的に照明(ライト)を点ける
このように「何々ならば…をする」、「何々で、そして、これこれだったら…をする」というような考え方を「論理(ロジック = logic)」と言います。そして、このような論理を電子回路で作ったものを「論理回路」と呼ぶのです!
さらに、上で書いたように「今は夜で、そして、部屋の中に人がいたら」のように、あること(今は夜だ)と別のこと(部屋の中に人がいる)が「両方」正しいときに何かをするには、先ほど紹介した「AND(アンド)」という論理回路を使います。回路図を次のように描きます。
この、ボート(小舟)を上からみたような記号の、左側の線(信号)は、AND 回路の入り口で、入力(にゅうりょく)と呼びます。右側の線(信号)は出口で、これを出力(しゅつりょく)と呼びます。
AND 回路では、入力の全てが「真(しん = 正しいということ)」のとき、出力から「真」という信号が出てきます。
また、AND 回路では複数の入力を描くことができます。上の回路図では入力信号が 2つですが、これを 3つにしたり、5つにしたりすることができるのです。その場合、全ての入力が真(正しいとき)、出力が真(正しい)になります。
一方で、出力は常に 1つです。AND 回路の外で信号を 2つに分岐(分ける)しても良いのですが、回路そのものとしては、出力は 1つです。
真と偽
さきほど、「真」という言葉をこっそり使いました。これをちゃんと説明しましょう。
論理回路では、あることが「正しいこと」「そうであること」を、真(しん)と呼びます。参考書によっては、これを H(エイチあるいはハイ)と書いてあることもありますが、正確には「真」と呼びます。ちなみに、英語では「true(トゥルー)」と言います。(技術者の方は、真と言うより、true と言うことが多いと思います。)
一方、あることが「正しくないこと」、「そうでないこと」は、偽(ぎ)と呼びます。これも、参考書によっては L(エルあるいはロー)と書いてあることもあります。こちらは、英語では「false(フォールス)」と言います。
論理回路は、伝える信号、判断の入力、判断の結果などを、全て「真か偽」で表します。例えば、いま、時計が午後 10時だとしましょう。そのとき、論理回路では「今は夜である」が「真」、つまり正しいことと考えます。逆に、時計が午前 8時だったら、「今は夜である」は正しくないので「偽」になります。
分かりますか? ちょっと難しいかも知れませんね。
いま、あなたが学校にいて、先生から「○○さんは、今朝ちゃんとご飯を食べてきましたか?」と聞かれたら、普通は「はい」あるいは「いいえ」と答えますね。論理回路の世界では、これを「真です」、あるいは「偽です」、というのです。つまりやさしくいうと、真とは「はい」のことで、偽とは「いいえ」ということになります。
「あいまい」は、ない!
論理回路の世界では、真でも偽でもない、あいまいな判断はありません。現実の世界では、「今は夜である」という論理があるとき、例えば午後 6時は、その論理が真か偽が決めにくいことがあります。しかし、論理回路を設計するときには、どこかで線を引くしかありません。たとえば、「午後 7時から午前 5時までを夜とする」というふうに、きっちり決める必要があります。論理回路では通常、「どちらでもない」という論理はありません。
よく、機械やコンピュータは融通(ゆうずう)が利かない、というような言い方をしますが、普通の論理回路は、このように真と偽しか判断できないので、そういうふうな言い方になるのですね。一方で、最近は人工知能(機械学習、AI)という研究が進んできて、今までの論理回路ではできないような、あいまいな判断をすることができるようになってきましたが、今回の勉強では、古くからの論理回路だけを考えましょう。
なお、このような、真か偽かしか扱えない論理(回路)を、難しい言葉では二値論理(にちろんり)と呼びます。
OR(オア)と NOT(ノット)
さて、AND 回路については分かりました。これ以外に重要な論理、また論理記号として、OR(オア)と NOT(ノット)があります。
AND 回路は、複数の入力の全てが真のときに出力が真となりますが、OR 回路では、入力のどれかが真だと、出力が真になります。AND 回路の働きを、「…で、そして、…だったら」と説明しましたが、OR 回路では、「…で、あるいは、…だったら」というように説明することができます。
以下に例を示します。AND 回路の記号は入力側がまっすぐな線、出力側が丸い形でしたが、OR 回路では、入力側を凹んだ丸い線、出力側をとがった丸い線で描きます。正しい形をしっかり覚えましょう。
さて。この OR 回路の出力では、どのようなことができるでしょうか。
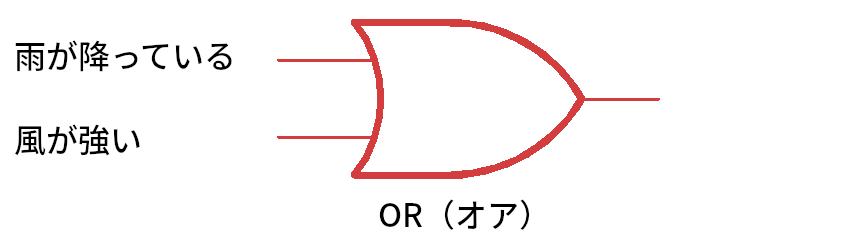
例えば、こんなことはどうでしょう? 雨が降っているか、あるいは風が強かったら、窓を自動的に閉めてくれる論理回路があったら便利ではないでしょうか? 雨が降っていて、そして風も強かったら、ではなく、どちらかだけでも、窓を閉めてくれると嬉しいですね。このようなとき、OR 回路を使います。「雨が降っている」か、あるいは、「風が強かった」ら、窓を閉める、というような回路という訳です。
OR 回路も AND 回路と同様、入力は複数あって良いです。出力は一つだけです。
最後が、NOT 回路です。インバータ(= inverter、反転器のこと)とも呼びます。
NOT 回路は、入力の論理(真か偽か)を、ひっくり返す働きがあります。つまり、入力が真だったら出力は偽に、入力が偽だったら、出力は真になります。あまのじゃくな回路ですね。
いま上の NOT 回路では、洗濯機が動いているとき、入力が真になりますが、そのとき、出力は偽になります。逆に、洗濯機が動いて「いない」とき、出力は真になります。この論理回路をうまく使うと、洗濯機が停まったらアラームを鳴らす、なんていう回路を作れそうですね。
真理値表
いままで説明してきたような論理回路の働きを、表で表すことができます。このような表を、真理値表(しんりちひょう)と言います。「まりちひょう」ではありませんよ。 🙂
AND 回路の真理値表
以下、見やすくするため、真を 1、偽を oと書くことにします。(論理回路では、数字の 1を真、0 を偽と表すことがよくあります。)
まず最初に、2入力の AND 回路です。
| 入力A | 入力B | 出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
2入力の AND では、入力の組み合わせは 2 × 2 で 4通りになります。
次は、3入力の AND 回路です。
| 入力A | 入力B | 入力C | 出力 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
3入力の AND では、入力の組み合わせは 2 × 2 × 2 で 8通りになります。
いずれの場合でも、AND 回路では、全ての入力が真(1)にならないと、出力が真(1)にならないことが分かります。
OR 回路の真理値表
まず最初に、2入力の OR 回路です。
| 入力A | 入力B | 出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
次は、3入力の OR 回路です。
| 入力A | 入力B | 入力C | 出力 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
OR 回路では、入力のどれか 1つが真(1)になると、出力が真(1)になることがよく分かりますね。
NOT 回路の真理値表
NOT 回路は、1入力しかありません。
| 入力 | 出力 |
|---|---|
| 0 | 1 |
| 1 | 0 |
真理値表は、このように論理回路記号(AND, OR, NOT)などの意味を説明するときによく使われますが、実際には、もっと複雑な回路の設計で重要な働きをします。
組み合わせ論理回路
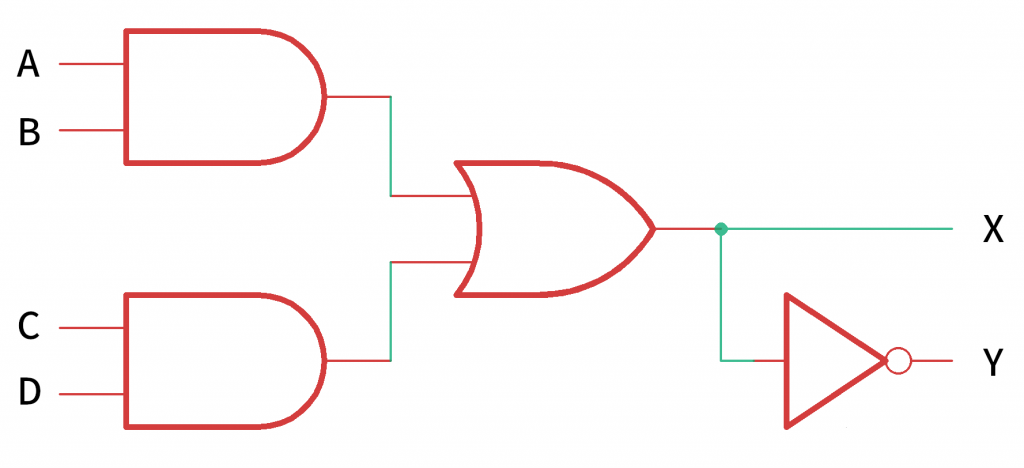
さて、ここまでは AND や OR 回路一つだけの回路を紹介しましたが、もちろん、これらの回路を複数繋いで複雑な回路を作ることができます。一つ例を示しましょう。なお、このような論理回路を「組み合わせ(論理)回路(combinational logic circuit)」と呼びます。
回路上のポチっとした小さな丸(●)は、ここで信号線が繋がっている、という意味です。なお、回路図が赤と緑で描き分けられていますが、これは回路図を作った CAD(キャド)ソフトの都合であって、回路図をこのような色で描かなくてはいけない、という意味ではありません。
さて、上の(複雑な)回路を言葉で表すと次のようになります。
(A かつ B)あるいは(C かつ D)ならば X は真である。X が真ならば Y は偽である。
なお、「A かつ B」というのは、「A が真で、かつ B が真である」を略した言い方です。また、「…ならば X が真である」という言い方も、「…ならば X である」と略すことができます。
次に、先ほど説明した真理値表でこの回路を見てみましょう。
| 入力A | 入力B | 入力C | 入力D | 出力X | 出力Y |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 |
どうでしょう? すぐには理解できないかも知れませんが、じっくり眺めていると、少しずつ分かるようになりますよ!
電気で論理回路を作るには
さて、いままで論理回路の信号を「真」とか「偽」とか言ってきましたが、実際に電気の仕組を使って論理回路を実現するにはどうしたら良いのでしょう?
電気の簡単な仕組については小学校 3〜4年生で習います。また、電圧(何ボルト)・電流(何アンペア)といった考え方を中学校 2年生で学びますね。多くの電子回路では、この「電圧」を使って「真」や「偽」を表します。
一般には(多くの場合は)、高い電圧で真、低い電圧で偽を表します。 また、電気で論理回路を説明するときには、普通は「真/偽」ではなく、このような電圧の考え方を使って、高い電圧を H(high = ハイ)、低い電圧を L(low = ロー)と呼ぶのが一般的です。
ただし注意点として、H が常に真を表すとは限らないということに注意してください。「信号が真であることを H(ハイ)で表そう」と決まりのとき、これを「H 能動(のうどう)あるいは active-high(アクティブ・ハイ)と呼びます。逆に、「信号が真であることを L(ロー)で表そう」という場合は、これを「L 能動」あるいは active-low(アクティブ・ロー)の信号と呼びます。
難しいですね。皆さんは、「普通は H(ハイ = 高い電圧)で真を表すけど、逆の場合もあるんだ」というくらいに覚えておけば OK です。
皆さんの中で、Arduino(アルデュイーノ)、PIC(ピック)、Raspberry Pi(ラズベリーパイあるいはラズパイ)といったマイコンボードを触ったことのある方がいるかも知れません。これらのマイコンは通常、5V(ボルト)あるいは 3.3V の電圧で動いていて、ある信号線(回路)に 5V(あるいは 3.3V)の電圧がかかっているとき、これを「H(ハイ)」としています。また、電圧が 0V(電圧がかかっていないということ)のとき、これを「L(ロー)」とします。
電子回路は多くの場合、電圧を低くするほど消費電流が少なくなる(つまり、電池が長持ちする)ので、最近は 5V でなく、3.3V、2.5V、1.8V といった電圧で動く電子回路やマイコンが増えています。しかし、皆さんがもし電子回路に触れるときは、だいたい、5V か 3.3V だと思って間違いないでしょう。
ちょっと難しい話(読み飛ばして良いです)
ところで、皆さんの中で注意深い方は心配することでしょう。
もし、5V で動く論理回路に、半分の 2.5V を入力したらどうなるの?
それは非常に良い(するどい)質問です! このように中途半端な電圧(正確には電位(でんい)と言います)を入力した場合、電気で動く論理回路では、これを H と判断するか L と判断するかは、「閾値(しきいち)」あるいはスレッシュホールド(= threshold)というもので決まります。あるいは、H か L を明確にできるように、閾値が決められている、と考えても良いでしょう。
具体的な閾値については、皆さんはここで覚える必要はありませんが(ネットで調べればすぐに分かります)、昔ながら(1980年代ころでしょうか)多く使われた、5V 動作の TTL(ティーティーエル, Transistor-Transistor Logic)と呼ばれるゲジゲジ論理 IC では、入力が 2V 以上ならば H、0.8V 以下ならば L、という決まり(設計)になっていました。
その間にある中途半端な電圧を入力した場合は、それは H と判断されるかも知れませんし、L と判断されるかも知れません。(それはちょうど、皆さんが授業中に少しだけ手を挙げてみたとき、先生は、あなたが手を挙げて質問しようとしていると判断するかも知れませんし、あるいはそうは思わないかも知れない、ということと似ています。)
ただし、このような中途半端な電圧を入力すると、論理回路が誤動作(誤った動き)をすることがあるので、そのような入力をしてはいけないことになっています。ただし普通は、すぐに IC やマイコンが壊れてしまうということはないので、あまり心配しなくて大丈夫です。
 (This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.)
(This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.)
余談: ところで、なぜ TTL の H 側にはマージン(余裕)が 5 – 2 = 3V もあるのに、L 側のマージンは 0.8V しかないんだ? と思われる方があるかも知れません。TTL という IC はバイポーラトランジスタという半導体技術で作られているのですが、入力閾値がベース・エミッタ間の PN 接合の順電圧で決まるため、このような非対称(H 側と L 側がアンバランスになっている)な特性になっているのだと思います。
一方で、最近よく使われているマイコン IC は TTL ではなく、C-MOS(シーモス)と呼ばれる半導体技術で作られていて、閾値は TTL のものと違います。たとえば、先ほど触れた Arduino(アルデュイーノ)と呼ばれるマイコンボードに搭載されている Atmel 社のマイコン(5V 動作の場合)では、入力が 3V 以上で H、1.5V 以下で L という決まりになっています。C-MOS の論理 IC では、「おおむね、電源電圧の 2/3 以上なら H、1/3 以下なら L」と覚えておくと分かりやすいでしょう。
はい、難しい話はここで終わりにします。
ようやく Minecraft(マイクラ)だ!
さて、これで終わりにしてしまうと、「えーーっ、マイクラの話を聞きたかったのに〜」という悲鳴が聞こえてきそうですので、マイクラでの論理回路の話を少しだけしましょう。
Minecraft(マイクラ)のブロック(アイテム)の中で、論理回路を作れそうなものとして、レッドストーンコンパレーター(以下、略してコンパレーターと呼びます)があります。コンパレーター(comparator)とは、日本語に訳すと「比較器(ひかくき。比べるもの)」という意味になります。コンパレーターには 2つの(正確には 3つ)入力があり、入ってくる 2つの信号を比べて出力を変化させる機能があります。
実は、マイクラには、レッドストーントーチの不思議な性質を利用して論理回路を組む方法があります。ネットで検索すると、おそらくそちらが見つかると思うのですが、今回はあくまでも、「電気信号を使って論理回路を作る原理(仕組)」を勉強するのが目的ですので、まずは基本的な考え方からスタートします。
ただし、大きな論理回路を作ろうとするとレッドストーントーチの性質を使ったほうがコンパクトな回路を描けることも確かです。次回以降、そのやり方も少しだけ紹介したいと思います。
まずは、以下のビデオを御覧ください。
コンパレーターって不思議なブロックですね。私は最初、ネットの情報(Minecraft Wiki など)を見ないで働きを理解しようとしたのですが、諦めました…。皆さんもぜひチャレンジしてください。
さて。コンパレーターのメイン(主)の入力は、上のビデオ(写真)で手前側にあります。そして、左右にサブ(副)の入力があります。左右の入力は同じ働きをするのですが、しばらくは左右の片方だけを使ったほうが、分かりやすくて良いでしょう。
ところで、この回路では、実はレッドストーンダストの回路の長さが重要なのです。前回までに説明したように、レッドストーンダストを伝わると、レッドストーン信号の強さが弱くなっていきます。
そうなんです。この回路では、メインの入力(手前側)の信号が、左側(あるいは右側)の入力よりも(少し)弱くないと、論理回路として働かないのです! この辺りの仕組は、次回説明したいと思います。
また余談: マイクラのレッドストーン回路は、とーってもよく考えられていると思います。レッドストーン回路は、実は「アナログ回路」なのですね。アナログ回路を使って論理回路を作る、というのは、本当に勉強になるものです。私が、若い電子技術者にマイクラのレッドストーン回路で
遊んで貰いたい、ではなくて、電子回路を復習して欲しい、というのは、こういう理由があるためです。
そうそう、一つだけ重要な注意があります。前回に説明したリピーターと同様に、コンパレーターの上には右クリックで操作できるスイッチがあります。スイッチが消えているときはコンパレーターとして働きますが、このスイッチを右クリックしてオンにすると(明かりが灯ります)、今度は「引き算器(subtracter)」という回路として働きます。しばらくの間は、このスイッチをオフのままで使ってくださいね。
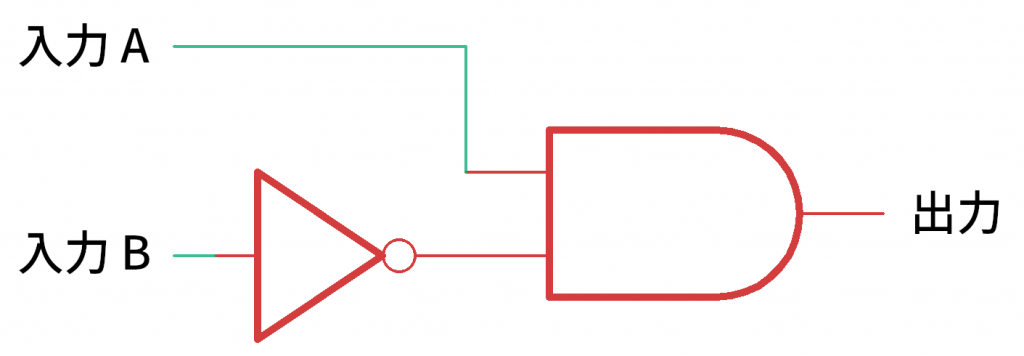
上のレッドストーン回路は、下の論理回路と同じ働きをします。入力 A は、ビデオの中に出てくる手前のレバー、入力 B は、左側に置いたレバーです。いずれも、レバーをオンにしたときが「真」になります。また、出力が真のとき、レッドストーンランプが灯ります。
ビデオの最後にもありますが、この回路の真理値表を書いておきましょう。
| 入力A | 入力B | 出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
つまり、先ほどのビデオに出てくるレッドストーン回路は、基本的には AND 回路なのですが、入力 B の真/偽が逆になっているのです。これは、上の論理回路図にあるように、入力 B が NOT 回路で反転している(ひっくり返っている)と考えると良いでしょう。つまり、入力 B が真だと、NOT 回路の出力は偽となり、AND 回路の下側の入力も偽となります。逆に、B が偽だと、NOT 回路の出力は真となり、AND 回路の下側の入力も真となります。
今回はここまで。皆さんも、コンパレーターにいろんなつなぎ方をして、このコンパレーターがどのように働いているのか調べてみると良いでしょう。答えは、次回! (いや、次回の次回になるかな??)
なお、以下の YouTube チャネルに御登録頂くと、新しい教材が公開された際にすぐ御覧頂けます。よろしくお願いいたします!